ollvm 算是日常逆向的过程中的一个难点，试想一下当你把程序拖进 ida 后那无穷无尽的 block 出现在面前的感受，这滋味一言难尽呐…

所以很有必要对 ollvm 的混淆与反混淆进行系统的学习，以便在未来实际生活中遇到时，不必慌忙的去 google 寻找答案.

文中的分析所用到的附件可以点这里下载哦 ollvm_bcf-fla-sub.zip

# 预备知识

llvm 是一个完整的编译器架构，作用可以理解为制作一个编译器，llvm 先将源码生成为与目标机器无关的 LLVM IR 代码，然后把 LLVMIR 代码先优化，再向目标机器的汇编语言而努力。经典编译器都可以分为前端、中层优化和后端：

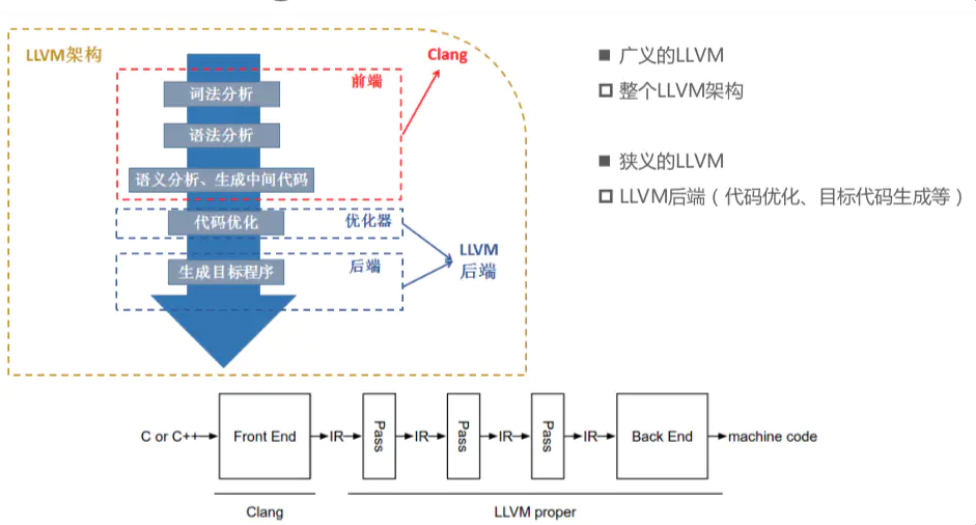
image-20230726095250772

从上图中可以看到 clang 是前端的一个套件，但在实际使用时，我们只可以感受到 clang，也只是在使用 clang，因为编译的时候，是调用 clang 或 clang++ 来编译源码。

而 ollvm 是基于 LLVM 的代码分支的代码混淆，在中间表示 IR 层，通过编写 pass（遍历一遍 IR，可以同时对它做一些操作）来混淆 IR，这样目标机器的汇编语言也就被混淆了

# ollvm 环境搭建

ollvm 搭建的环境为

  • ubuntu22.04

# 下载 ollvm 4.0 源码

git clone -b llvm-4.0 --depth=1 https://github.com/obfuscator-llvm/obfuscator.git

# 安装 docker

sudo apt install docker.io

# 安装编译 ollvm 的 docker 环境

sudo docker pull nickdiego/ollvm-build

# 编译 ollvm

# 下载编译脚本

git clone --depth=1 https://github.com/oacia/docker-ollvm.git

# 编译

ollvm-build.sh 后面跟的参数是 ollvm的源码目录

sudo docker-ollvm/ollvm-build.sh /home/oacia/Desktop/obfuscator/

# 创建硬链接

sudo ln ./obfuscator/build_release/bin/* /usr/bin/

创建完成硬链接后，使用该命令来检测 clang 是否可用

clang --version

# 使用测试代码尝试编译

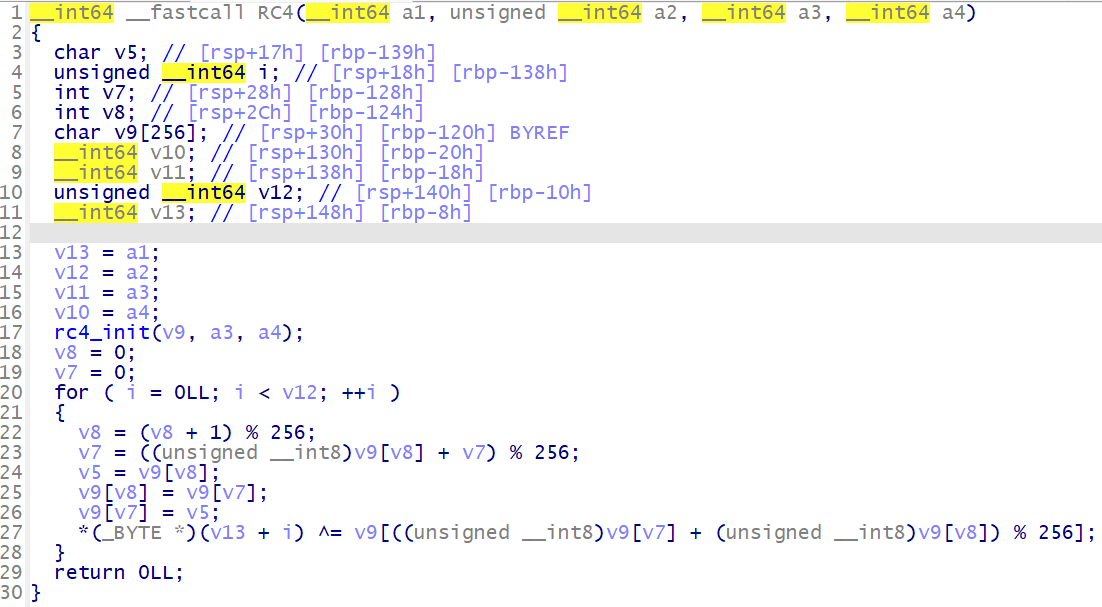
使用一个简单的 RC4 加密来作为测试代码， 该代码将在后续 ollvm 的三种混淆中继续使用

//test.c
#include<stdio.h>
/*
RC4 初始化函数
*/
void rc4_init(unsigned char* s, unsigned char* key, unsigned long Len_k)
{
	int i = 0, j = 0;
	char k[256] = { 0 };
	unsigned char tmp = 0;
	for (i = 0; i < 256; i++) {
		s[i] = i;
		k[i] = key[i % Len_k];
	}
	for (i = 0; i < 256; i++) {
		j = (j + s[i] + k[i]) % 256;
		tmp = s[i];
		s[i] = s[j];
		s[j] = tmp;
	}
}
/*
RC4 加解密函数
unsigned char* Data     加解密的数据
unsigned long Len_D     加解密数据的长度
unsigned char* key      密钥
unsigned long Len_k     密钥长度
*/
void RC4(unsigned char* Data, unsigned long Len_D, unsigned char* key, unsigned long Len_k) // 加解密
{
	unsigned char s[256];
	rc4_init(s, key, Len_k);
	int i = 0, j = 0, t = 0;
	unsigned long k = 0;
	unsigned char tmp;
	for (k = 0; k < Len_D; k++) {
		i = (i + 1) % 256;
		j = (j + s[i]) % 256;
		tmp = s[i];
		s[i] = s[j];
		s[j] = tmp;
		t = (s[i] + s[j]) % 256;
		Data[k] = Data[k] ^ s[t];
	}
}
void RC4encrypt(unsigned char* Data, unsigned long Len_D, unsigned char* key, unsigned long Len_k) {
	RC4(Data, Len_D, key, Len_k);
}
void RC4decrypt(unsigned char* Data, unsigned long Len_D, unsigned char* key, unsigned long Len_k) {
	RC4(Data, Len_D, key, Len_k);
}
int main()
{
	// 字符串密钥
	unsigned char key[] = "secret";
	unsigned long key_len = sizeof(key) - 1;// 字符串最后还有一个 '/0' 所以需要 - 1
	// 数组密钥
	//unsigned char key[] = {'s','e','c','r','e','t'};
	//unsigned long key_len = sizeof(key);
	unsigned char data[] = { 116, 104, 105, 115, 32, 105, 115, 32, 82, 67, 52, 44, 111, 97, 99, 105, 97 };
	
	// 对明文进行加密
	RC4encrypt(data, sizeof(data), key, key_len);
	for (int i = 0; i < sizeof(data); i++)
	{
		printf("%d, ", data[i]);
	}
	printf("\n");
	
	// 对密文进行解密
	RC4encrypt(data, sizeof(data), key, key_len);
	for (int i = 0; i < sizeof(data); i++)
	{
		printf("%c", data[i]);
	}
	printf("\n");
	return 0;
}
/*
153, 94, 187, 111, 162, 205, 165, 134, 96, 136, 143, 240, 156, 135, 150, 94, 204,
this is RC4,oacia
*/
运行如下命令进行编译


clang test.c -o test



    

  • 如果提示 fatal error: ‘stdio.h’ file not found
    • 



​	尝试下载 g++ 和 gcc


sudo apt-get install g++
sudo apt-get install gcc
    

  • 如果提示 fatal error: 'stddef.h’或者’stdarg.h’等 file not found
    • 



使用该命令复制 clang 所需的头文件到 /usr/include/ ,  cp -r -i  后面跟的参数为 ollvm的源码目录/build_release/lib/clang/4.0.1/include/. , 这个文件夹内包含了 clang  编译器所需的头文件


cp -r -i /home/oacia/Desktop/obfuscator/build_release/lib/clang/4.0.1/include/. /usr/include/
如果提示有重名文件的话，最好先对 /usr/include  内的重名文件作好备份，然后去掉 -i  参数重新进行复制头文件操作


# 虚假控制流 BCF (Bogus Control Flow)


# 原理


虚假控制流混淆通过加入包含不透明谓词的条件跳转（也就是跳转与否在运行之前就已经确定的跳转，但 IDA 无法分析）和不可达的基本块，来干扰 IDA 的控制流分析和 F5 反汇编。


所谓的不透明谓词，例如


if(x>10 && x<=10){
    goto Label1;
}
对于这类表达式，我们可以很明显的看到， x>10 && x<=10  是永假式，所以 goto Label1  这个跳转永远不会被执行，但是对于 IDA 来说可不是这个样子，在静态分析的时候，IDA 并不知道 x  的值是多少，所以说这类虚假控制流就会干扰我们的静态分析.


# ollvm 的 BCF 混淆


使用下列命令对代码进行 BCF 混淆


clang -mllvm -bcf -mllvm -bcf_loop=3 -mllvm -bcf_prob=40 test.c -o test-bcf
可用选项：


    

  • -mllvm -bcf  : 激活虚假控制流
    • 

  • -mllvm -bcf_loop=3  : 混淆次数，这里一个函数会被混淆 3 次，默认为 1
    • 

  • -mllvm -bcf_prob=40  : 每个基本块被混淆的概率，这里每个基本块被混淆的概率为 40%，默认为 30 %
    • 





可以发现在 BCF 混淆之后，函数的控制流明显复杂了许多


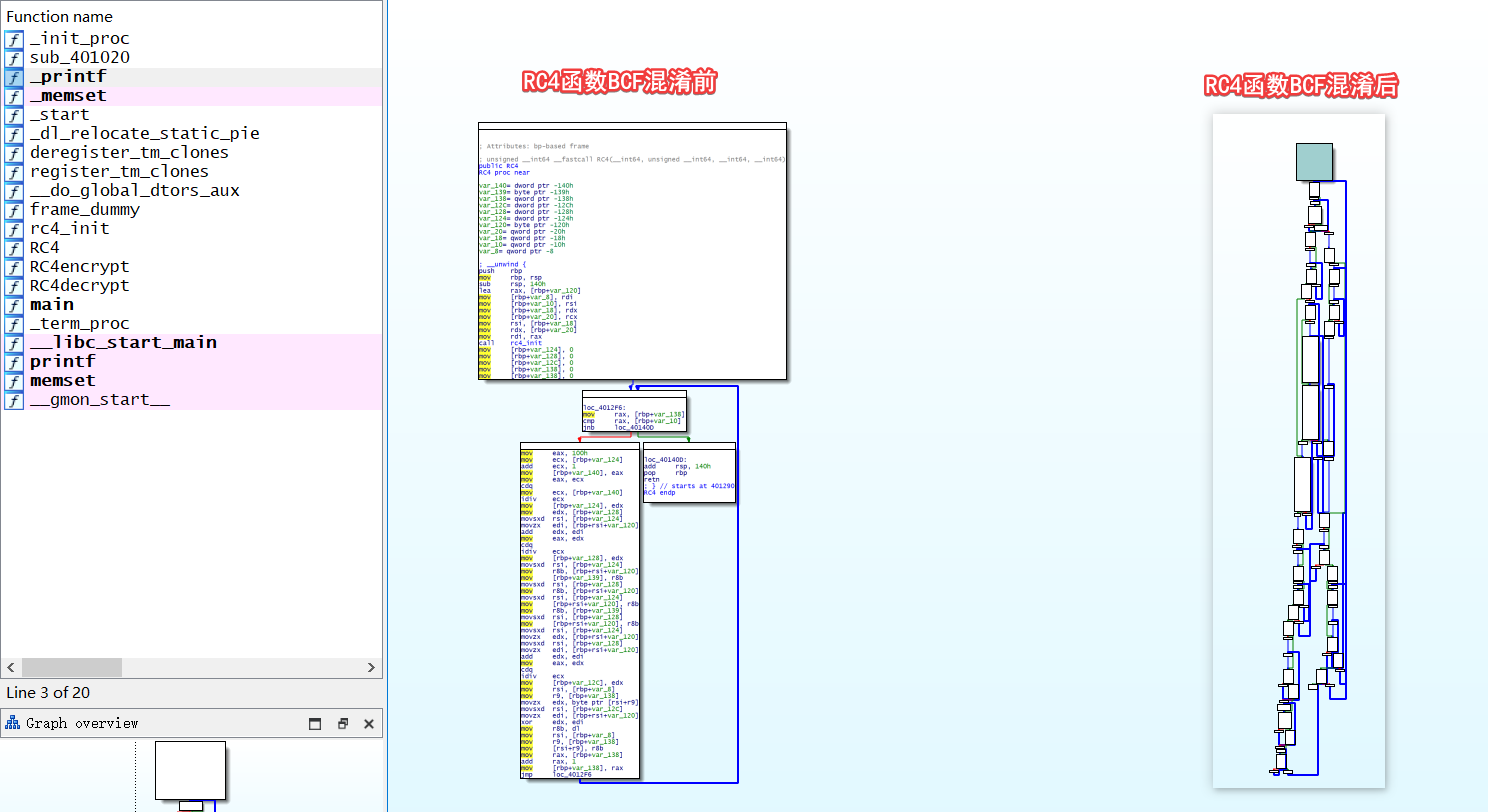
image-20230727162443249


打开 BCF 混淆之后 IDA 的伪代码，发现多了许多的 while , if  表达式，伪代码变得十分复杂，也让我们无法一眼就可以看出这是何种加密


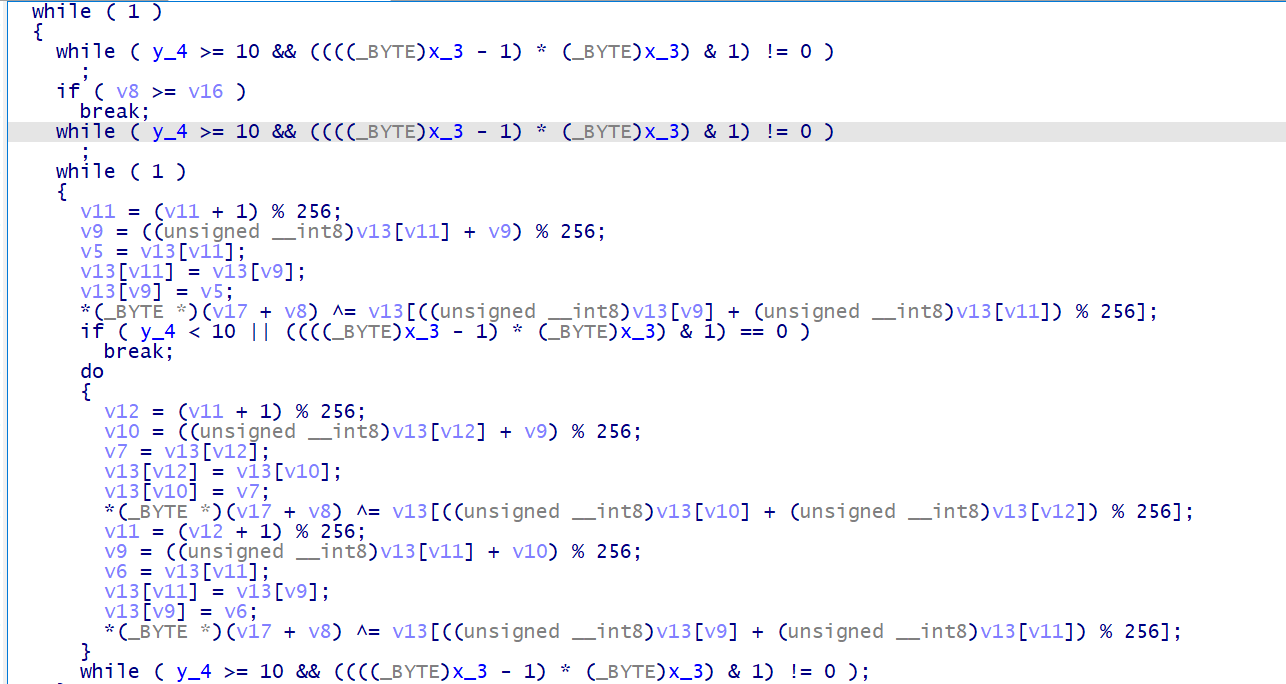
image-20230727162652645


# ollvm 的 BCF 反混淆


铺垫了这么长的时间，终于要来到本篇文章的第一个有趣的环节，BCF 的反混淆了


我们往上看 while  内的表达式 y_4 >= 10 && (((x_3 - 1) * x_3) & 1) != 0 , 在这个式子中， (x_3 - 1) * x_3)  的值永远为偶数，所以 (x_3 - 1) * x_3) & 1  永远返回 0 , 不等号左边 y_4 >= 10 && (((x_3 - 1) * x_3) & 1) , 因为是用逻辑与 &&  作为连接词，所以左侧的表达式其实为永假式， y_4 >= 10 && (((x_3 - 1) * x_3) & 1) != 0  永远不成立


对于 BCF, 有 3 种思路可以帮助我们去进行反混淆


# 思路一 将全局变量赋值并将 segment 设为只读


IDA 其实是有死代码消除 (DCE, Dead Code Elimination) 的，但是由于 y_4 , x_3  被定义为了全局变量，在静态分析时，IDA 不知道这个表达式的值是多少，所以 IDA 也不敢轻易的就把这段代码给消除了 (万一把重要的代码也给消除掉了那逆向人员真的要 *** 了)


但是如果我们把这个变量的值定下来，并且将变量所在的 segment  设为 只读 ，那这个变量值在没运行前也变不了，IDA 不就可以自己算出来这个表达式的值是多少了嘛，这样那些没有用的跳转 IDA 就可以自动优化了


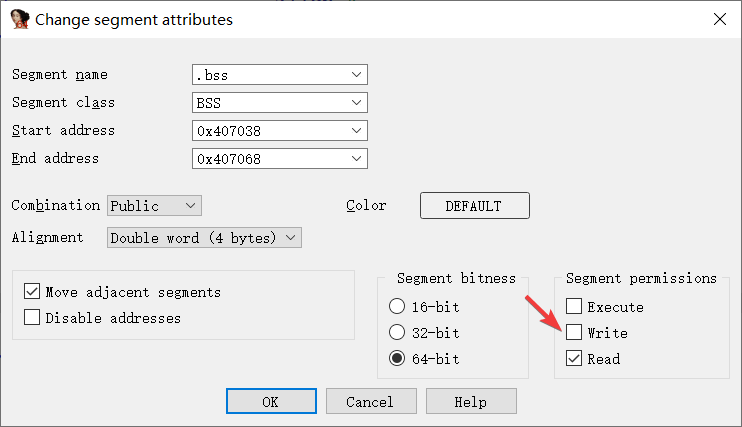
所以我们先双击 x_3  跳转到 x_3  的地址


image-20230727185741834


然后按下 Alt+S 或者 Edit->Segments->Edit segment...  来改变不透明谓词所在的 segment 的读写属性，如图将 Write  复选框取消勾选， .bss段 就设为只读了


image-20230727203726728


光是这样还不够，因为 .bss段 中的变量还没有被赋过值，所以我们还需要 patch 这个段来固定 .bss段 内变量的值


一个变量一个变量去 patch 显然显得有些麻烦，所以我们可以直接编写 IDApython 脚本来实现一步到位的效果，并且对于常规的 ollvm 的 bcf 混淆来说，bcf 的不透明谓词都是处于 .bss段 中。如果不透明谓词定义在其他段中，将 IDApython 中的代码做出相对应的修改即可


import ida_segment
import ida_bytes
seg = ida_segment.get_segm_by_name('.bss')
for ea in range(seg.start_ea, seg.end_ea,4):
    ida_bytes.patch_bytes(ea, int(2).to_bytes(4,'little'))
'''
seg.perm: 由三位二进制数表示,例如一个segment为可读,不可写,不可执行,则seg.perm = 0b100
(seg.perm >> 2)&1: Read
(seg.perm >> 1)&1: Write
(seg.perm >> 0)&1: Execute
'''
seg.perm = 0b100
# 思路二 使用 d810 去除 BCF


d810 中内置了很多的不透明谓词表达式，它的匹配器也是非常的厉害完全可以做到去除虚假控制流


在 Edit->plugins->D-810  打开之后，选择 default_unflattening_switch_case.json  之后点击 start , 即可做到对不透明谓词的去除并还原控制流


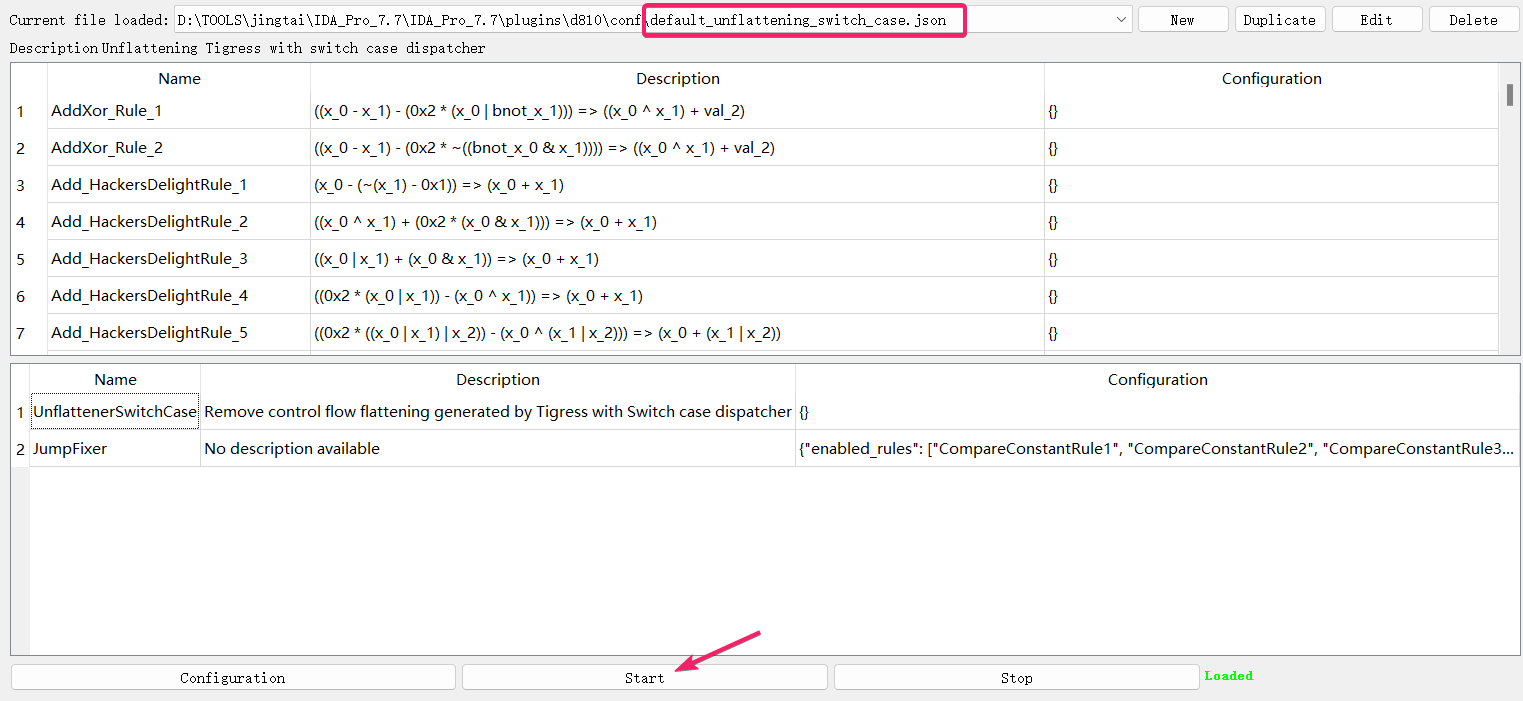
image-20240711153007836


还原后的效果如下，可以发现和原本的代码基本是一样的了


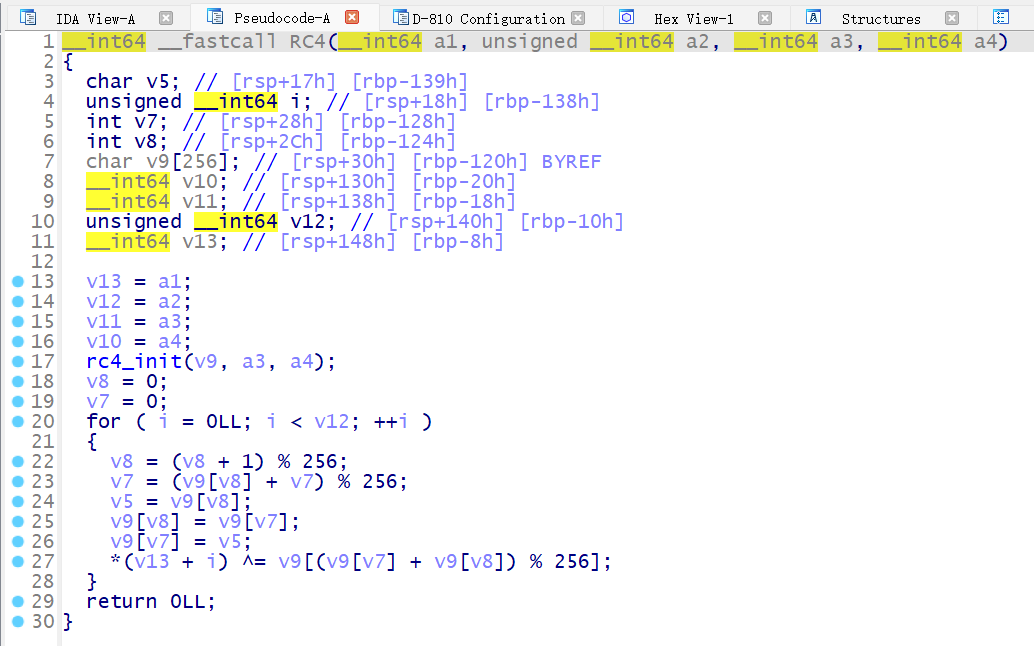
image-20240711153057510


当然如果发现有一些恒定值的不透明谓词表达式 d810 没有识别到无法去除的话，我们也可以手动添加规则让 D810 进行匹配来消除 BCF


例如对于这个表达式 ((x_0>=10 && x_10<10)==false) == True , 我们可以先在 \plugins\d810\conf\xxx.json  里面添加我们自己的规则


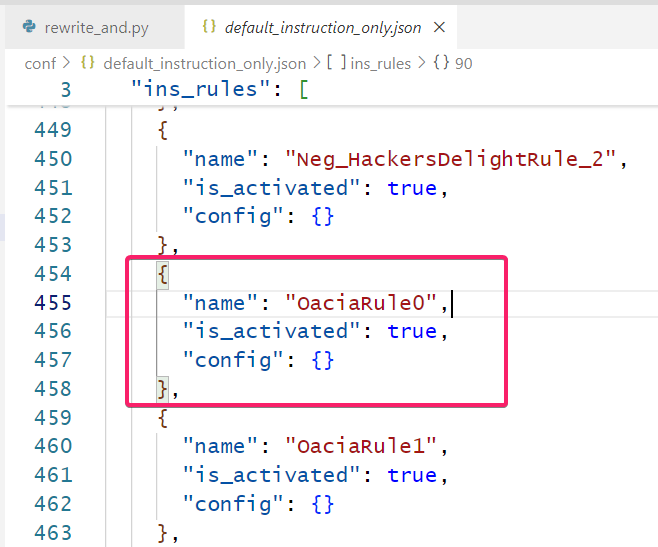
image-20240712102230251


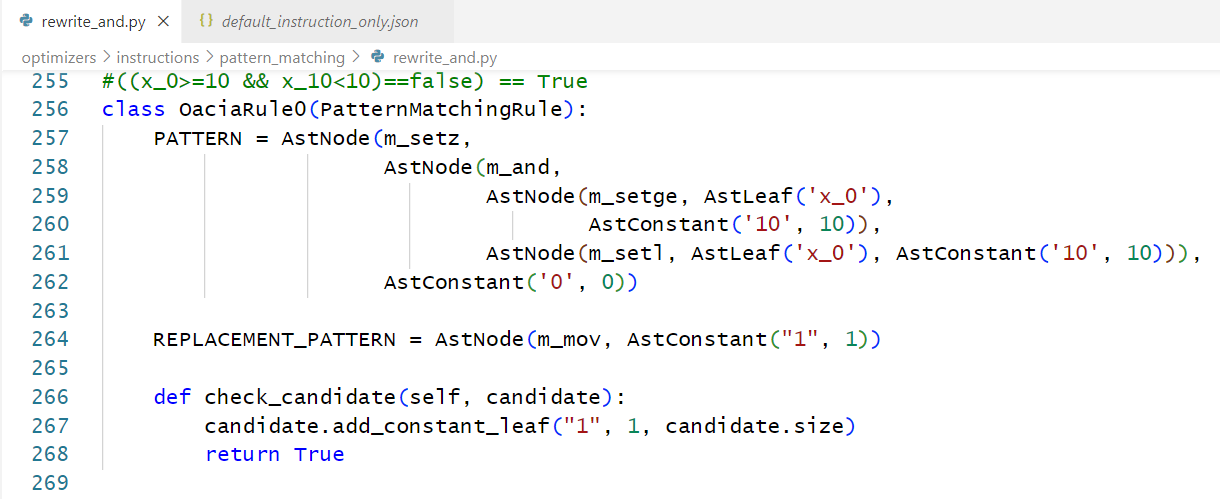
随后来到 plugins\d810\optimizers\instructions\pattern_matching\rewrite_and.py  中加一个我们自己的类 OaciaRule0 , 这样就可以完成一个自定义规则的导入啦


image-20240712102331669


# 思路三 使用 idapython patch 不透明谓词


在思路一中，我们通过对不透明谓词变量进行交叉引用找到了它们所在的 segment, 并通过将全局变量赋值并将 segment 设为只读的方法消除了 BCF, 但是其实我们还可以用另外的一种方式去消除 bcf, 就是在汇编中将不透明谓词直接 patch 掉


例如对于该不透明谓词 x_9 , y_10 , 它的 c 表达式为 y_10 >= 10 && ((((_BYTE)x_9 - 1) * (_BYTE)x_9) & 1) != 0


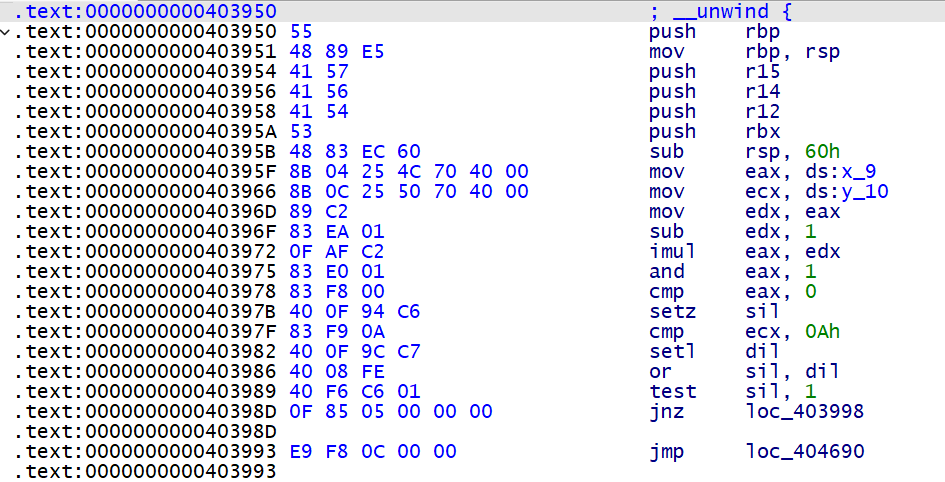
image-20240712103021119


我们要做的就是让 mov     eax, ds:x_9  改成 mov     eax, 0 , 这样就可以做到消除 BCF 的目的


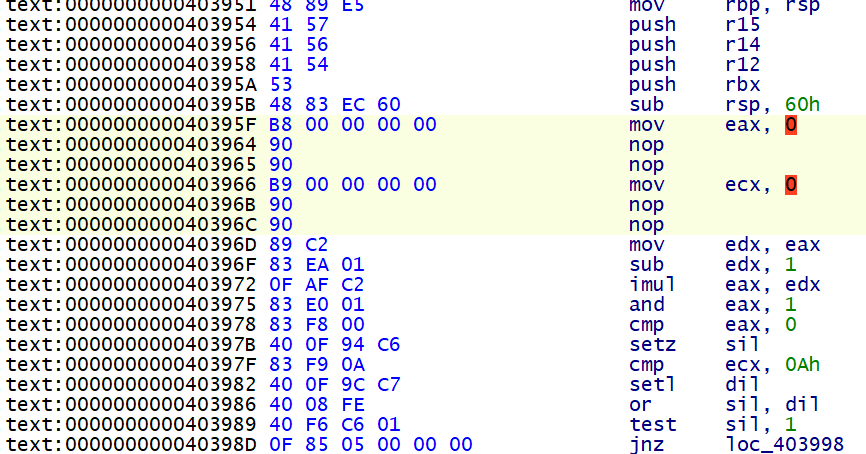
image-20240712103224264


但是这样一个一个改过去显得十分的麻烦，所以我们可以用 ida python, 通过找到不透明谓词的所有交叉引用的方式来批量修改


# 去除虚假控制流 idapython 脚本
import ida_xref
import ida_idaapi
from ida_bytes import get_bytes, patch_bytes
 
# 将 mov 寄存器，不透明谓词 修改为 mov 寄存器，0
def do_patch(ea):
    if get_bytes(ea, 1) == b"\x8B": # mov eax-edi, dword
        reg = (ord(get_bytes(ea + 1, 1)) & 0b00111000) >> 3
        patch_bytes(ea, (0xB8 + reg).to_bytes(1,'little') + b'\x00\x00\x00\x00\x90\x90')
    else:
        print('error')
 
# 不透明谓词在.bss 段的范围
seg = ida_segment.get_segm_by_name('.bss')
start = seg.start_ea
end = seg.end_ea
 
for addr in range(start,end,4):
    ref = ida_xref.get_first_dref_to(addr)
    print(hex(addr).center(20,'-'))
    # 获取所有交叉引用
    while(ref != ida_idaapi.BADADDR):
        do_patch(ref)
        print('patch at ' + hex(ref))
        ref = ida_xref.get_next_dref_to(addr, ref)
    print('-' * 20)
这样 BCF 就被去掉啦


image-20240712104339001


# 指令替换（SUB）


# 原理


指令替换（Instruction Substitution）是一种代码混淆技术，用于将程序中的原始指令替换为等效但更难理解和还原的指令序列。通过指令替换，可以增加程序的复杂性和抵抗逆向工程的能力。


它的本质其实就是数学公式的简化，例如 (x + y) - 2 * (x & y) -> x ^ y  (过去学离散数学感觉做的就是这种样子的…)


# ollvm 的 SUB 混淆


使用下面的命令对代码进行 SUB 混淆


clang -mllvm -sub -mllvm -sub_loop=3 test-sub.c -o test-sub
可用选项


    

  • -mllvm -sub  : 激活指令替换
    • 

  • -mllvm -sub_loop=3 : 混淆次数，这里一个函数会被混淆 3 次，默认为 1 次
    • 



经过指令替换后，代码明显变长了很多


image-20240712105930858


# ollvm 的 SUB 反混淆


# 思路一 使用 d810 去除 SUB


D810 太猛了！这里又用到了 D810


还是和去除 BCF 反混淆一样，我们直接跑一下 d810, 虽然还是有一些部分没有去掉，但是看起来已经很清晰了，因为指令替换不影响程序整体的执行逻辑，所以我想剩下的一点点 SUB 应该难不倒逆向的同学吧～


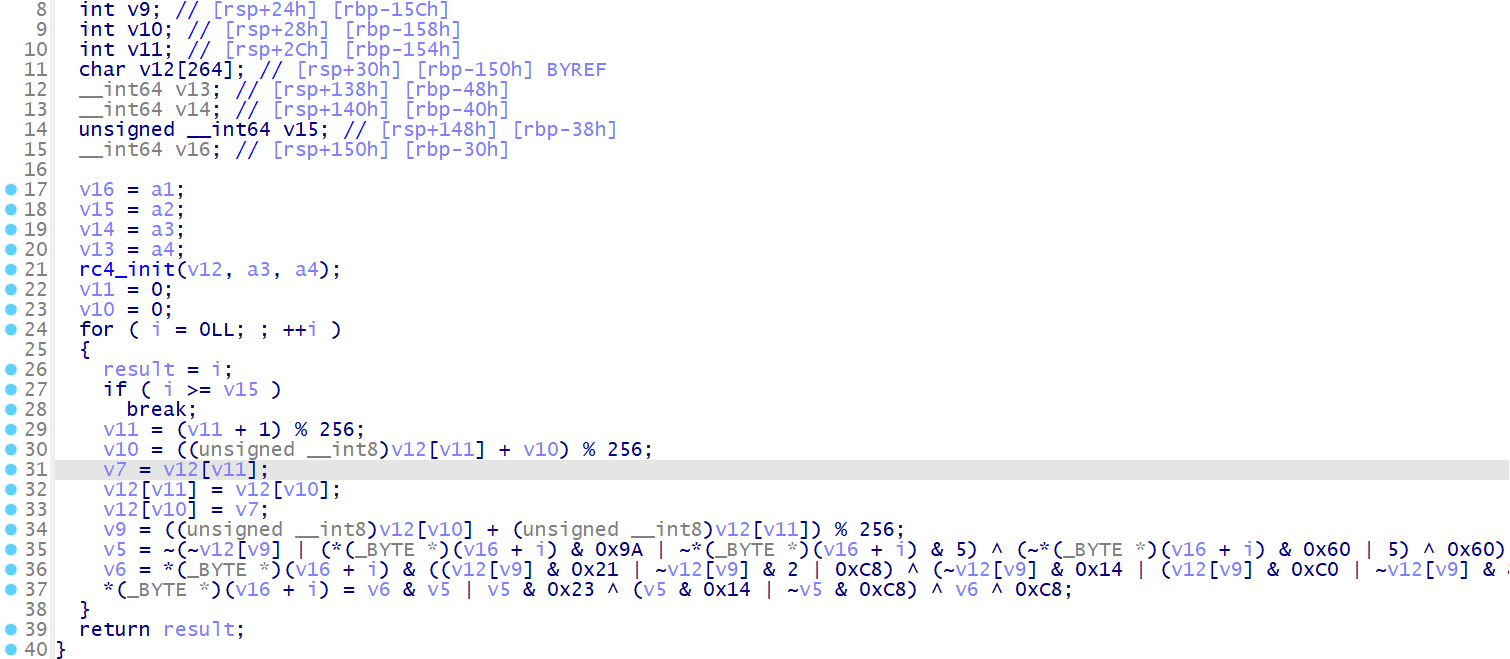
image-20240712110422977


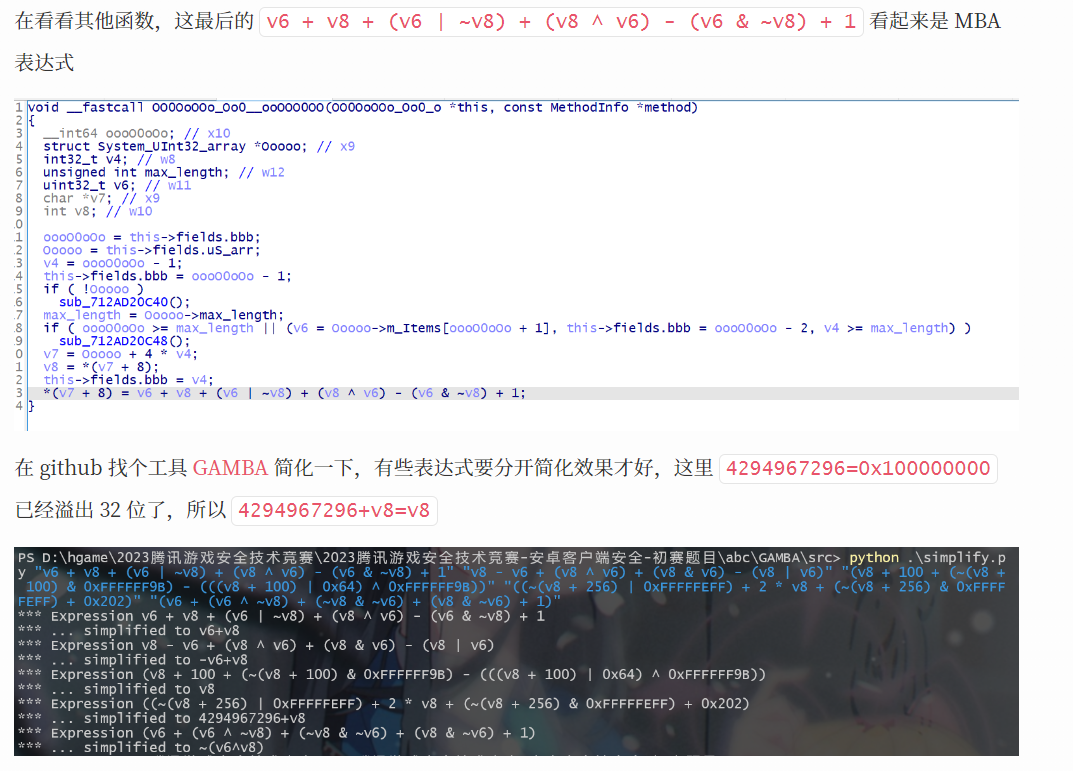
# 思路二 使用 GAMBA 简化复杂的 SUB 表达式


这个思路二其实就是思路一那一点点未解决的 SUB 的补充，对于一些复杂的表达式来说，github 上的开源工具 GAMBA 可以很好的帮助我们简化


具体可以参考细品 sec2023 安卓赛题中的 加密三 vm 指令分析


image-20240712111021857


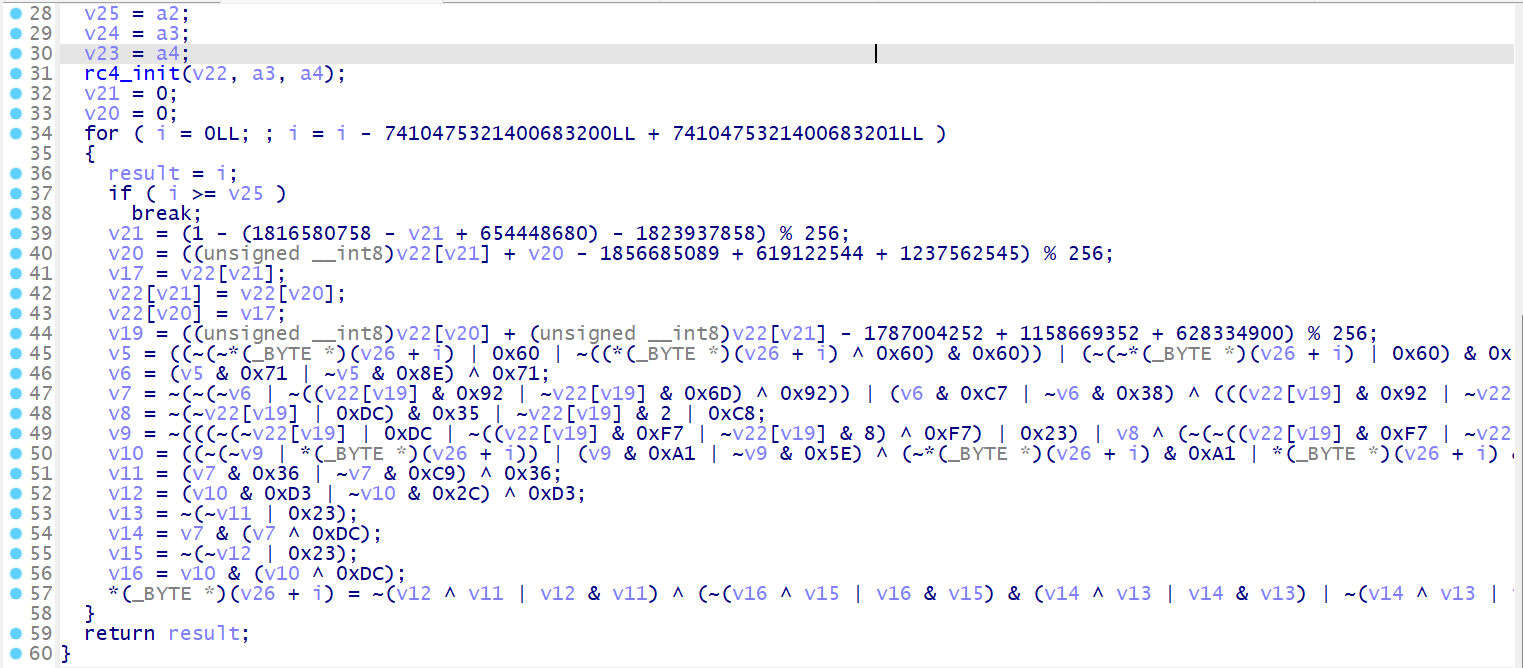
# 控制流平坦化（FLA）


# 原理


控制流平坦化 (control flow flattening) 的基本思想主要是通过一个主分发器来控制程序基本块的执行流程，例如下图是正常的执行流程


img


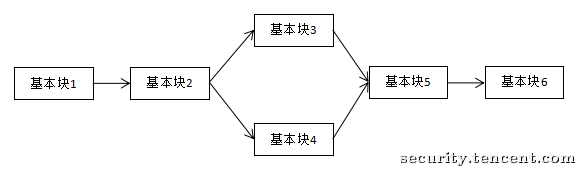
经过控制流平坦化后的执行流程就如下图


img


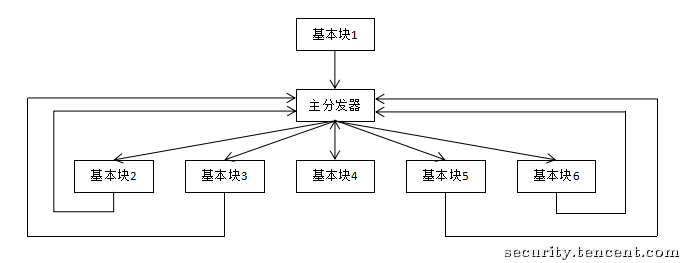
这样可以模糊基本块之间的前后关系


此图是一个经典的控制流平坦化 CFG


img


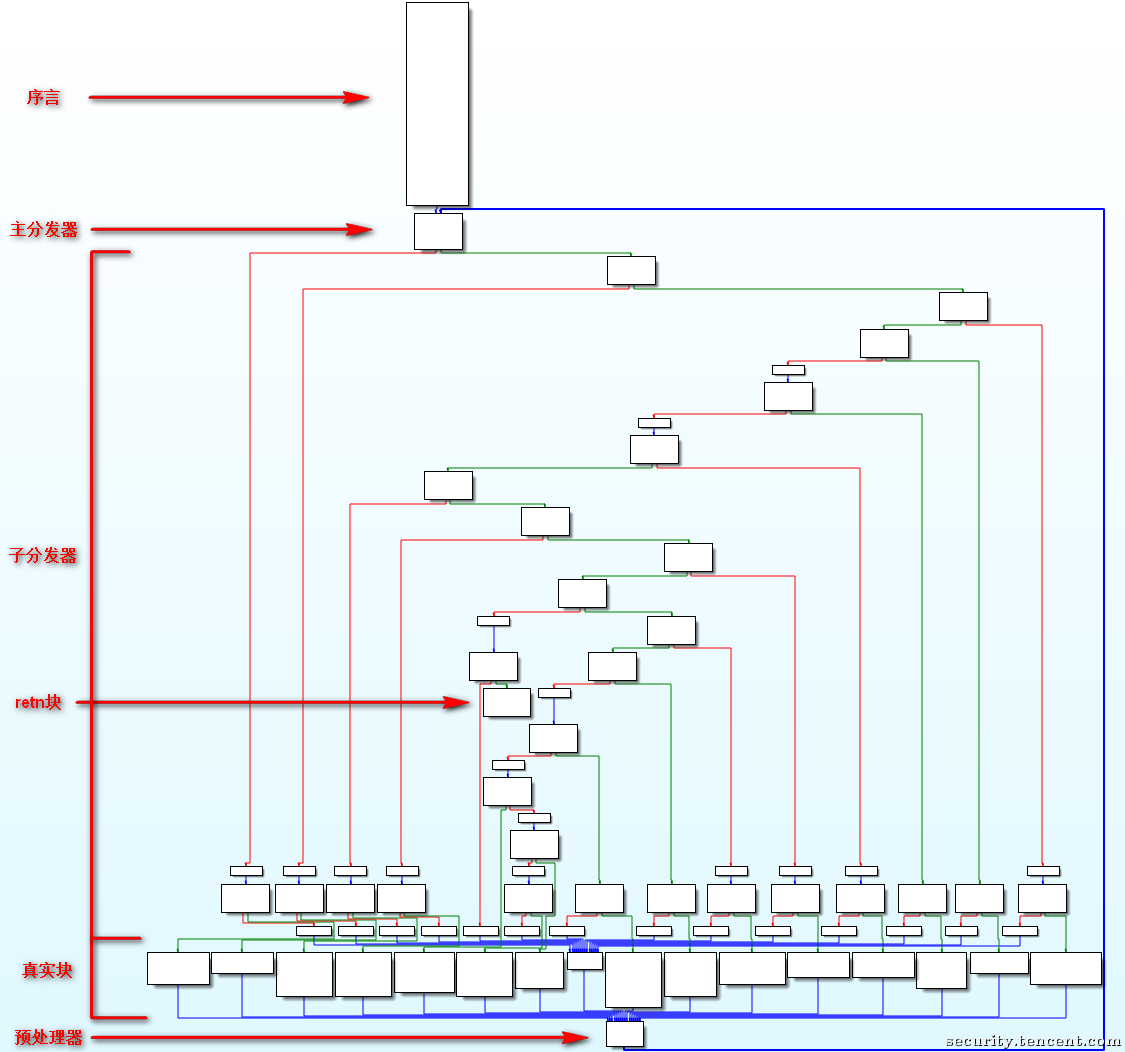
其中


    

  • 序言：函数的第一个执行的基本块
    • 

  • 主 (子) 分发器：控制程序跳转到下一个待执行的基本块
    • 

  • retn 块：函数出口
    • 

  • 真实块：混淆前的基本块，程序真正执行工作的块
    • 

  • 预处理器：跳转到主分发器
    • 



# ollvm 的 FLA 混淆


使用如下命令即可完成 fla 混淆


clang -mllvm -fla -mllvm -split -mllvm -split_num=3 test-fla.c -o test-fla
可用选项：


    

  • -mllvm -fla : 激活控制流平坦化
    • 

  • -mllvm -split : 激活基本块分割
    • 

  • -mllvm -split_num=3 : 指定基本块分割的数目
    • 



经过控制流平坦化之后，函数的逻辑已经很难看清楚了


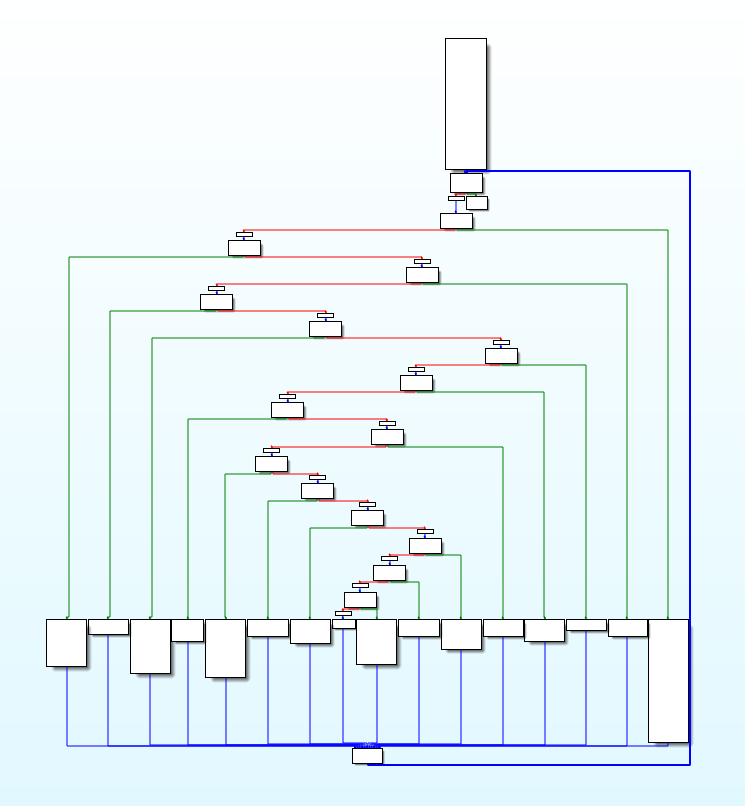
image-20240712132834341


# ollvm 的 FLA 反混淆


想要定位各个块其实很简单，对于经典的 ollvm 来说，各个块之间有如下规则 (要是魔改的话就具体情况具体分析啦)


    

  1. 找到序言块，这是整个函数的入口
    2. 

  2. 序言块的后继是主分发器
    3. 

  3. 主分发器的前驱有两个，除了序言块外，另一个块就是预处理器
    4. 

  4. 预处理器的前驱是真实块
    5. 

  5. 除此之外的其他块是子分发器
    6. 



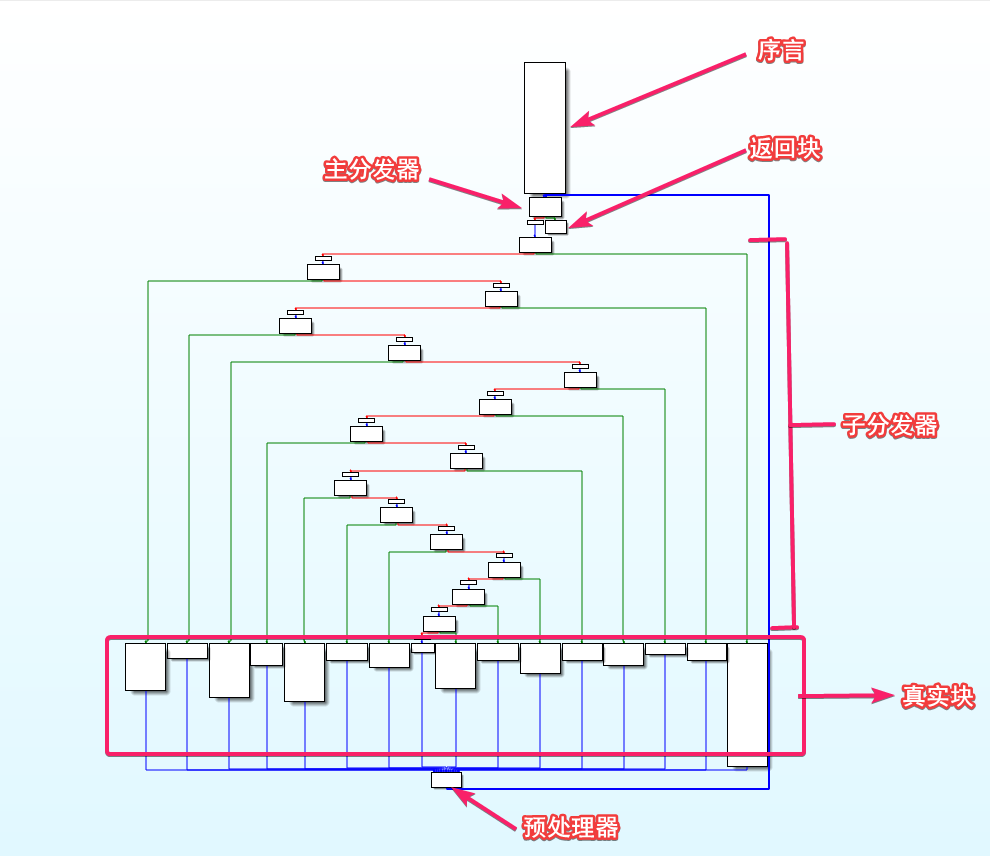
image-20240712132814751


想要反控制流平坦化，我们只需要做 3 步


    

  1. 找到真实块。我们可以手动找真实块；可以用 idapython 通过各个块之间的联系通过一定的规则找真实块；可以用 unicorn 或 angr 得到函数的 CFG, 利用规则匹配出真实块… 方法多种多样，但是核心都是找到真实块，除真实块和序言块外，其余的块都是虚假块，我们需要 NOP 掉他们
    2. 

  2. 得到真实块之间的联系。我们主要想知道分支跳转的另一个分支，它究竟跳到了什么地方去的呢？所以这一步我们必须得让代码运行起来，它把控制流给混淆了，我们要是不把代码跑起来咋知道控制流嘞？可以用模拟执行，也可以在真机调试打断点 trace, 核心都是为了找到真实块之间的调用关系
    3. 

  3. 得到了真实块之间的联系之后，我们只需要在每个真实块的末尾，用跳转汇编指令将每个真实块像串糖葫芦一样串起来，控制流平坦化就修复好啦～
    4. 



所以开始我们的第一步找到真实块和虚假块，对于标准的 ollvm 来说，观察得知预处理器的前驱都是真实块，所以我们写出如下的 idapython 脚本


import idaapi
import idc
target_func = 0x401E80#需要反控制流平坦化的函数的地址
Preprocessor_block = 0x402697#ollvm 中预处理器的地址，这个是通过观察 ida 中的 CFG 得到的，预处理器的前驱都是真实块
True_blocks = []#真实块列表
Fake_blocks = []#所有块的列表
f_block = idaapi.FlowChart(idaapi.get_func(0x401E80), flags=idaapi.FC_PREDS)
for block in f_block:
    if block.start_ea==Preprocessor_block:#预处理器块的前驱都是真实块
        #but 预处理器是虚假块
        Fake_blocks.append((block.start_ea,idc.prev_head(block.end_ea)))
        print("find ture block!")
        tbs = block.preds()
        for tb in tbs:
            #print (hex (tb.start_ea),hex (idc.prev_head (tb.end_ea)))# 获取块的开始 / 结束地址
            True_blocks.append((tb.start_ea,idc.prev_head(tb.end_ea)))
    elif not [x for x in block.succs()]:#返回块没有后继
        print("find ret block!")
        True_blocks.append((block.start_ea,idc.prev_head(block.end_ea)))
    # 序言块不作为虚假块处理
    elif block.start_ea!=target_func:
        #print(hex(block.start_ea),hex(idc.prev_head(block.end_ea)))
        Fake_blocks.append((block.start_ea,idc.prev_head(block.end_ea)))
print('true block:')
print('tbs =',True_blocks)
print('fake block:')
print('fbs =',Fake_blocks)
之后就是要得到真实块之间的联系啦，这里我使用 unicorn 来模拟执行得到真实块的调用关系，这里要注意的是因为我们只对一个函数中真实块的前后调用进行模拟执行，所以是不需要跳转到其他函数中的，遇到 call  指令直接将 pc 强制改成下一行汇编的地址，同时也要注意内存访问异常的情况直接通过 uc.hook_add(UC_HOOK_MEM_UNMAPPED|UC_HOOK_INTR, hook_mem_access)  进行忽略


通过这个 unicorn 脚本模拟执行，我们得到了分支跳转时下一个要跳转的真实块地址，以及此时的 ZF 标志位，这个标志位可是有着大用，通过这个标志位我们就可以知道究竟是 jz  跳转还是 jnz  跳转啦


# code for test-fla.elf
from unicorn import *
from unicorn.x86_const import *
from keystone import *  # pip install keystone-engine
from capstone import *  # pip install capstone
# import networkx as nx #pip install networkx
# import matplotlib.pyplot as plt  # pip install matplotlib
BASE = 0x400000
CODE = BASE + 0x0
CODE_SIZE = 0x100000
STACK = 0x7F00000000
STACK_SIZE = 0x100000
FS = 0x7FF0000000
FS_SIZE = 0x100000
ks = Ks(KS_ARCH_X86, KS_MODE_64)  # 汇编引擎
uc = Uc(UC_ARCH_X86, UC_MODE_64)  # 模拟执行引擎
cs = Cs(CS_ARCH_X86, CS_MODE_64)  # 反汇编引擎
# g=nx.Graph ()# 创建空的无向图
# g=nx.DiGraph ()# 创建空的有向图
tbs = [(4204176, 4204182), (4203066, 4203066), (4203071, 4203098), (4203103, 4203157), (4203162, 4203314),
       (4203319, 4203341), (4203346, 4203366), (4203371, 4203398), (4203403, 4203428), (4203433, 4203457),
       (4203462, 4203490), (4203495, 4203514), (4203519, 4203558), (4203563, 4203585), (4203590, 4203609),
       (4203614, 4203636), (4203641, 4203651), (4203656, 4203689), (4203694, 4203737), (4203742, 4203776),
       (4203781, 4203804), (4203809, 4203831), (4203836, 4203856), (4203861, 4203888), (4203893, 4203918),
       (4203923, 4203957), (4203962, 4203981), (4203986, 4204025), (4204030, 4204040), (4204045, 4204067),
       (4204072, 4204091), (4204096, 4204118), (4204123, 4204133), (4204138, 4204171)]
tb_call = []
main_addr = 0x00000000000401E80
main_end = 0x0000000000040269C
def hook_code(uc: unicorn.Uc, address, size, user_data):
    # print(hex(address))
    for i in cs.disasm(CODE_DATA[address - BASE:address - BASE + size], address):
        if i.mnemonic == "call":  # 因为只是针对单个函数的控制流，所以我们并不需要跳转到其他的函数里面
            print(f"find call at {hex(address)}, jump...")
            uc.reg_write(UC_X86_REG_RIP, address + size)
        elif i.mnemonic == "ret":
            print("find ret block, emu stop~")
            uc.emu_stop()
            print("block emu path↓↓↓↓")
            print(tb_call)
            # for i in range(len(tb_call)-1):
            #     g.add_edge(tb_call[i],tb_call[i+1])
            # Plot it
            # nx.draw(g, with_labels=True)
            # nx.write_gml(g,'./test-fla.gml')
    for tb in tbs:
        if address == tb[1]:
            # print (uc.reg_read (UC_X86_REG_FLAGS))#ZF 标志位在第 6 位
            ZF_flag = (uc.reg_read(UC_X86_REG_FLAGS) & 0b1000000) >> 6
            #print("ZF=", ZF_flag)
            tb_call.append((tb, ZF_flag))
            break
def hook_mem_access(uc: unicorn.Uc, type, address, size, value, userdata):
    pc = uc.reg_read(UC_X86_REG_RSP)  # UC_ARM64_REG_PC
    print('pc:%x type:%d addr:%x size:%x' % (pc, type, address, size))
    # uc.emu_stop()
    return True
def inituc(uc):
    uc.mem_map(CODE, CODE_SIZE, UC_PROT_ALL)
    uc.mem_map(STACK, STACK_SIZE, UC_PROT_ALL)
    uc.mem_write(CODE, CODE_DATA)
    uc.reg_write(UC_X86_REG_RSP, STACK + 0x1000)
    uc.hook_add(UC_HOOK_CODE, hook_code)
    uc.hook_add(UC_HOOK_MEM_UNMAPPED | UC_HOOK_INTR, hook_mem_access)
def init_graph():
    for tb in tbs:
        g.add_node(tb[1])
with open('./test-fla', 'rb') as f:
    CODE_DATA = f.read()
inituc(uc)
try:
    uc.emu_start(main_addr, main_end)
except Exception as e:
    print(e)
之后再去写一个 idapython 脚本将真实块串起来就可以啦，我们观察标准的 ollvm 混淆后的文件后发现，其实真实块所处的位置是连续的，比如有这两个真实块，虽然他们跳转的地址都是 loc_402697  预处理器的位置，但是这两个真实块没有分支跳转，所以说我们只需要将 jmp loc_402697  nop 掉，就完成了无分支跳转真实块的串联，而麻烦的只是分支跳转，我们由模拟执行后已经得到了分支跳转时的 ZF 标志位，通过该标志位我们将将 jmp 改成为零跳转 (jz) 亦或是非零跳转 (jnz)


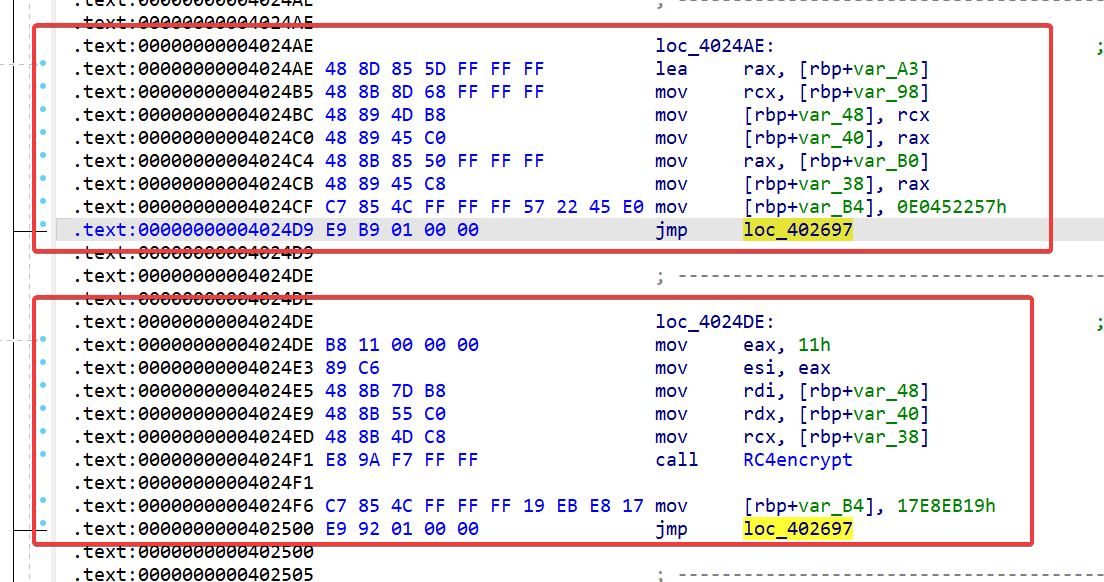
image-20240719234623318


写一下 patch 脚本，修复成功～


import idaapi
import ida_bytes
import idc
from keystone import *
ks = Ks(KS_ARCH_X86, KS_MODE_64)  # 汇编引擎
def jmp_patch(start, target, j_code="jmp"):
    global debug
    patch_byte, count = ks.asm(f"{j_code} {hex(target)}", addr=start)
    patch_byte = bytes(patch_byte) + b'\x00' * (idc.get_item_size(start) - len(patch_byte))
    print(hex(start), f"{j_code} {hex(target)}", patch_byte)
    ida_bytes.patch_bytes(start, patch_byte)
def patch_nop(addr, endaddr):
    #print(f"Patching from {addr} to {endaddr}")
    while addr < endaddr:
        ida_bytes.patch_byte(addr, 0x90)
        addr += 1
def patch_nop_line(addr):
    patch_nop(addr,addr+idc.get_item_size(addr))
preamble_block = 0x401E8B  # 序言块的地址
internal_reg = '[rbp+var_B4]'#中间变量的名称，遇到这个想都不用想直接 NOP
# 格式: ((块的起始地址，块的结束地址),ZF 标志位)
tb_path = [((4203071, 4203098), 0), ((4203103, 4203157), 0), ((4203162, 4203314), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 0), ((4203403, 4203428), 0), ((4203433, 4203457), 1),
           ((4203462, 4203490), 0), ((4203495, 4203514), 1), ((4203519, 4203558), 1), ((4203563, 4203585), 1),
           ((4203590, 4203609), 0), ((4203614, 4203636), 1), ((4203641, 4203651), 1), ((4203319, 4203341), 1),
           ((4203346, 4203366), 1), ((4203371, 4203398), 1), ((4203403, 4203428), 1), ((4203656, 4203689), 1),
           ((4203694, 4203737), 1), ((4203742, 4203776), 1), ((4203781, 4203804), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 0), ((4203893, 4203918), 0), ((4203923, 4203957), 0),
           ((4203962, 4203981), 1), ((4203986, 4204025), 1), ((4204030, 4204040), 1), ((4204045, 4204067), 1),
           ((4204072, 4204091), 0), ((4204096, 4204118), 1), ((4204123, 4204133), 1), ((4203809, 4203831), 1),
           ((4203836, 4203856), 1), ((4203861, 4203888), 1), ((4203893, 4203918), 1), ((4204138, 4204171), 1)]
tbs = [(4204176, 4204182), (4203066, 4203066), (4203071, 4203098), (4203103, 4203157), (4203162, 4203314), (4203319, 4203341), (4203346, 4203366), (4203371, 4203398), (4203403, 4203428), (4203433, 4203457), (4203462, 4203490), (4203495, 4203514), (4203519, 4203558), (4203563, 4203585), (4203590, 4203609), (4203614, 4203636), (4203641, 4203651), (4203656, 4203689), (4203694, 4203737), (4203742, 4203776), (4203781, 4203804), (4203809, 4203831), (4203836, 4203856), (4203861, 4203888), (4203893, 4203918), (4203923, 4203957), (4203962, 4203981), (4203986, 4204025), (4204030, 4204040), (4204045, 4204067), (4204072, 4204091), (4204096, 4204118), (4204123, 4204133), (4204138, 4204171)]
fbs = [(4202133, 4202159), (4202165, 4202165), (4202170, 4202187), (4202193, 4202193), (4202198, 4202215), (4202221, 4202221), (4202226, 4202243), (4202249, 4202249), (4202254, 4202271), (4202277, 4202277), (4202282, 4202299), (4202305, 4202305), (4202310, 4202327), (4202333, 4202333), (4202338, 4202355), (4202361, 4202361), (4202366, 4202383), (4202389, 4202389), (4202394, 4202411), (4202417, 4202417), (4202422, 4202439), (4202445, 4202445), (4202450, 4202467), (4202473, 4202473), (4202478, 4202495), (4202501, 4202501), (4202506, 4202523), (4202529, 4202529), (4202534, 4202551), (4202557, 4202557), (4202562, 4202579), (4202585, 4202585), (4202590, 4202607), (4202613, 4202613), (4202618, 4202635), (4202641, 4202641), (4202646, 4202663), (4202669, 4202669), (4202674, 4202691), (4202697, 4202697), (4202702, 4202719), (4202725, 4202725), (4202730, 4202747), (4202753, 4202753), (4202758, 4202775), (4202781, 4202781), (4202786, 4202803), (4202809, 4202809), (4202814, 4202831), (4202837, 4202837), (4202842, 4202859), (4202865, 4202865), (4202870, 4202887), (4202893, 4202893), (4202898, 4202915), (4202921, 4202921), (4202926, 4202943), (4202949, 4202949), (4202954, 4202971), (4202977, 4202977), (4202982, 4202999), (4203005, 4203005), (4203010, 4203027), (4203033, 4203033), (4203038, 4203055), (4203061, 4203061), (4203066, 4203066), (4203071, 4203098), (4203103, 4203157), (4203162, 4203314), (4203319, 4203341), (4203346, 4203366), (4203371, 4203398), (4203403, 4203428), (4203433, 4203457), (4203462, 4203490), (4203495, 4203514), (4203519, 4203558), (4203563, 4203585), (4203590, 4203609), (4203614, 4203636), (4203641, 4203651), (4203656, 4203689), (4203694, 4203737), (4203742, 4203776), (4203781, 4203804), (4203809, 4203831), (4203836, 4203856), (4203861, 4203888), (4203893, 4203918), (4203923, 4203957), (4203962, 4203981), (4203986, 4204025), (4204030, 4204040), (4204045, 4204067), (4204072, 4204091), (4204096, 4204118), (4204123, 4204133), (4204138, 4204171), (4204183, 4204183)]
block_info = {}  #判断有没有 patch 结束
for i in range(len(tbs)):
    block_info[tbs[i][0]] = {'finish': 0,'ret':0}
#nop 掉所有虚假块
for fb in fbs:
    patch_nop(fb[1], fb[1] + idc.get_item_size(fb[1]))
for tb in tbs:
    dont_patch = False
    current_addr = tb[0]
    while current_addr <= tb[1]:
        # print(hex(current_addr),idc.GetDisasm(current_addr))
        if "cmov" in idc.print_insn_mnem(current_addr):
            #cmov 指令会影响分支跳转，所以这里直接 patch 掉
            patch_nop_line(current_addr)
            dont_patch = True
            # print(hex(current_addr),hex(tb_path[i][0]))
        elif internal_reg in idc.print_operand(current_addr, 0):
            print('find internal_reg!')
            patch_nop_line(current_addr)
        elif 'ret' in idc.print_insn_mnem(current_addr):
            block_info[tb[0]]['ret'] = 1
            dont_patch = True
        current_addr = idc.next_head(current_addr)
    if not dont_patch:
        patch_nop_line(tb[1])
        block_info[tb[0]]['finish'] = 1
# 序言块 -> 第一个真实块 patch
jmp_patch(preamble_block, tb_path[0][0][0])
for i in range(len(tb_path) - 1):
    # 不是返回块，也未完成 patch, 剩下的指令都是有分支跳转的.
    if block_info[tb_path[i][0][0]]['finish'] == 0 and not block_info[tb_path[i][0][0]]['ret']:
        ZF = tb_path[i][1]
        #当要跳转的块和当前块不连续时，这个分支跳转才修复完成
        if not idc.next_head(tb_path[i][0][1]) == tb_path[i + 1][0][0]:
            block_info[tb_path[i][0][0]]['finish'] = 1
            j_code = ('jnz', 'jz')
            jmp_patch(tb_path[i][0][1], tb_path[i + 1][0][0], j_code[ZF])
patch 完之后看一下，这个代码也太好看了吧哈哈哈！ (●'◡'●)


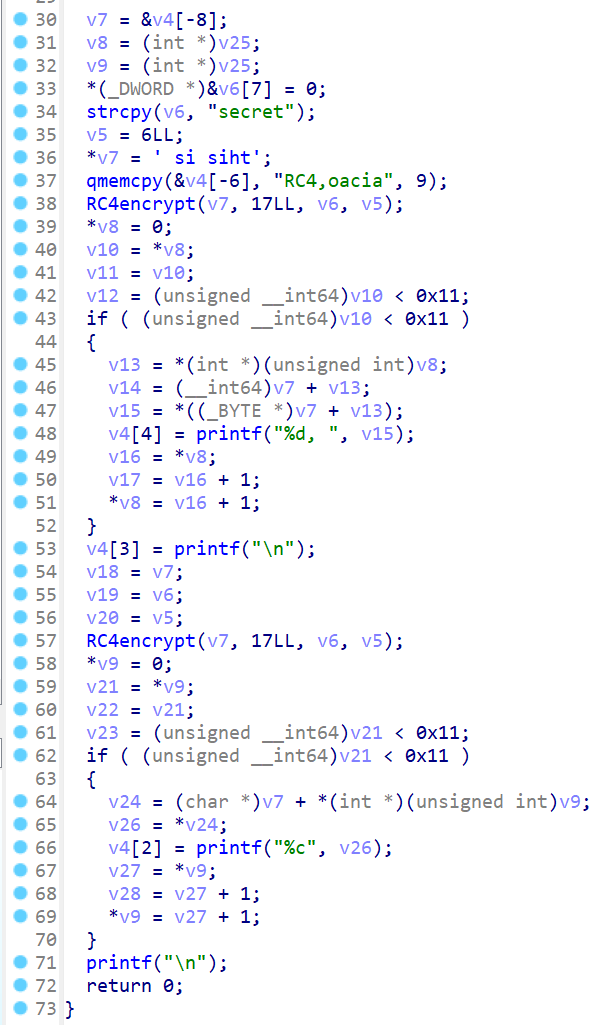
image-20240720005911998


小小总结一下，感觉 ollvm 的控制流平坦化去混淆原来那么简单呐～去年 sec2023 安卓赛题的 CESL-BR  混淆和 CEST-BR  混淆的反混淆 idapython 脚本可真是把我写昏过去了 (倒)


# 参考资料


    

  • 

    ollvm 快速学习
    

    • 

  • 

    跟着铁头干混淆 3 ubuntu 下用 docker 编译 ollvm (保证成功)
    

    • 

  • 

    OLLVM 混淆学习（0）—— 环境搭建及混淆初体验
    

    • 

  • 

    利用 angr 符号执行去除虚假控制流
    

    • 

  • 

    [原创] Android APP 漏洞之战（14）——Ollvm 混淆与反混淆
    

    • 

  • 

    利用符号执行去除控制流平坦化
    

    • 

  • 

    代码混淆与反混淆学习 - 第一弹
    

    • 



      

          
      

  


   


    

  
    
      
    
    更新于
    
  
  
      
        
      
      阅读次数
      
      次